Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the (ring of integers of the) algebraic number field. More specifically, it is related to the volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified.
The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic formulas such as the functional equation of the Dedekind zeta function of K, and the analytic class number formula for K. An old theorem of Hermite states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem, and the subject of current research.[1]
The discriminant of K can be referred to as the absolute discriminant of K to distinguish it from the relative discriminant of an extension K/L of number fields. The latter is an ideal in the ring of integers of L, and like the absolute discriminant it indicates which primes are ramified in K/L. It is a generalization of the absolute discriminant allowing for L to be bigger than Q; in fact, when L = Q, the relative discriminant of K/Q is the principal ideal of Z generated by the absolute discriminant of K.
Contents |
Definition
Let K be an algebraic number field, and let OK be its ring of integers. Let b1, ..., bn be an integral basis of OK (i.e. a basis as a Z-module), and let {σ1, ..., σn} be the set of embeddings of K into the complex numbers (i.e. ring homomorphisms K → C). The discriminant of K is the square of the determinant of the n by n matrix B whose (i,j)-entry is σi(bj). Symbolically,
Equivalently, the trace from K to Q can be used. Specifically, define the trace form to be the matrix whose (i,j)-entry is TrK/Q(bibj). This matrix equals BTB, so the discriminant of K is the determinant of this matrix.
Examples
- Quadratic number fields: let d be a square-free integer, then the discriminant of
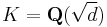 is
is
-
- An integer that occurs as the discriminant of a quadratic number field is called a fundamental discriminant.[2]
- Cyclotomic fields: let n > 2 be an integer, let ζn be a primitive nth root of unity, and let Kn = Q(ζn) be the nth cyclotomic field. The discriminant of Kn is given by[3]
-
- where
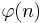 is Euler's totient function, and the product in the denominator is over primes p dividing n.
is Euler's totient function, and the product in the denominator is over primes p dividing n.
- Power bases: In the case where the ring of integers has a power integral basis, that is, can be written as OK = Z[α], the discriminant of K is equal to the discriminant of the minimal polynomial of α. To see this, one can chose the integral basis of OK to be b1 = 1, b2 = α, b3 = α2, ..., bn = αn−1. Then, the matrix in the definition is the Vandermonde matrix associated to αi = σi(α), whose determinant squared is
-
- which is exactly the definition of the discriminant of the minimal polynomial.
- Let K = Q(α) be the number field obtained by adjoining a root α of the polynomial x3 − x2 − 2x − 8. This is Richard Dedekind's original example of a number field whose ring of integers does not possess a power basis. An integral basis is given by {1, α, α(α + 1)/2} and the discriminant of K is −503.[4][5]
- Repeated discriminants: the discriminant of a quadratic field uniquely identifies it, but this is not true, in general, for higher-degree number fields. For example, there are two non-isomorphic cubic fields of discriminant 3969. They are obtained by adjoining a root of the polynomial x3 − 21x + 28 or x3 − 21x − 35, respectively.[6]
Basic results
- The sign of the discriminant is (−1)r2 where r2 is the number of complex places of K.[7]
- A prime p ramifies in K if, and only if, p divides ΔK .[8]
- Stickelberger's Theorem:[9]
- Minkowski bound:[10] Let n denote the degree of the extension K/Q and r2 the number of complex places of K, then
-
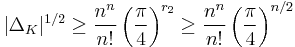 .
.
- Minkowski's Theorem:[11] If K is not Q, then |ΔK| > 1 (this follows directly from the Minkowski bound).
- Hermite's Theorem:[12] Let N be a positive integer. There are only finitely many algebraic number fields K with ΔK < N.
History
The definition of the discriminant of a general algebraic number field, K, was given by Dedekind in 1871.[13] At this point, he already knew the relationship between the discriminant and ramification.[14]
Hermite's theorem predates the general definition of the discriminant with Charles Hermite publishing a proof of it in 1857.[15] In 1877, Alexander von Brill determined the sign of the discriminant.[16] Leopold Kronecker first stated Minkowski's theorem in 1882,[17] though the first proof was given by Hermann Minkowski in 1891.[18] In the same year, Minkowski published his bound on the discriminant.[19] Near the end of the nineteenth century, Ludwig Stickelberger obtained his theorem on the residue of the discriminant modulo four.[20][21]
Relative discriminant
The discriminant defined above is sometimes referred to as the absolute discriminant of K to distinguish it from the relative discriminant ΔK/L of an extension of number fields K/L, which is an ideal in OL. The relative discriminant is defined in a fashion similar to the absolute discriminant, but must take into account that ideals in OL may not be principal and that there may not be an integral basis of K/L. Let {σ1, ..., σn} be the set of embeddings of K into C which are the identity on L. If b1, ..., bn is any basis of K over L, let d(b1, ..., bn) be the square of the determinant of the n by n matrix whose (i,j)-entry is σi(bj). Then, the relative discriminant of K/L is the ideal generated by the d(b1, ..., bn) as {b1, ..., bn} varies over all bases of K/L with the property that bi ∈ OK for all i. Alternatively, the relative discriminant of K/L is the norm of the different of K/L.[22] When L = Q, the relative discriminant ΔK/Q is the principal ideal of Z generated by the absolute discriminant ΔK . In a tower of fields K/L/F the relative discriminants are related by
where 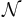 denotes relative norm.[23]
denotes relative norm.[23]
Ramification
The relative discriminant regulates the ramification data of the field extension K/L. A prime ideal p of L ramifies in K if, and only if, it divides the relative discriminant ΔK/L. An extension is unramified if, and only if, the discriminant is the unit ideal.[22] The Minkowski bound above shows that there are no non-trivial unramified extensions of Q. Fields larger than Q may have unramified extensions, for example, for any field with class number greater than one, its Hilbert class field is a non-trivial unramified extension.
Root discriminant
The root discriminant of a number field, K, of degree n, often denoted rdK, is defined as the n-th root of the absolute value of the (absolute) discriminant of K.[24] The relation between relative discriminants in a tower of fields shows that the root discriminant does not change in an unramified extension.
Relation to other quantities
- When embedded into
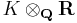 , the volume of the fundamental domain of OK is
, the volume of the fundamental domain of OK is 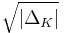 (sometimes a different measure is used and the volume obtained is
(sometimes a different measure is used and the volume obtained is 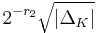 , where r2 is the number of complex places of K).
, where r2 is the number of complex places of K). - Due to its appearance in this volume, the discriminant also appears in the functional equation of the Dedekind zeta function of K, and hence in the analytic class number formula, and the Brauer-Siegel theorem.
- The relative discriminant of K/L is the Artin conductor of the regular representation of the Galois group of K/L. This provides a relation to the Artin conductors of the characters of the Galois group of K/L, called the conductor-discriminant formula.[25]
Notes
- ^ Cohen, Diaz y Diaz & Olivier 2002
- ^ Definition 5.1.2 of Cohen 1993
- ^ Proposition 2.7 of Washington 1997
- ^ Dedekind 1878, pp. 30–31
- ^ Narkiewicz 2004, p. 64
- ^ Cohen 1993, Theorem 6.4.6
- ^ Lemma 2.2 of Washington 1997
- ^ Corollary III.2.12 of Neukirch 1999
- ^ Exercise I.2.7 of Neukirch 1999
- ^ Proposition III.2.14 of Neukirch 1999
- ^ Theorem III.2.17 of Neukirch 1999
- ^ Theorem III.2.16 of Neukirch 1999
- ^ a b Dedekind's supplement X of the second edition of Dirichlet's Vorlesungen über Zahlentheorie (Dedekind 1871)
- ^ Bourbaki 1994
- ^ Hermite 1857.
- ^ Brill 1877.
- ^ Kronecker 1882.
- ^ Minkowski 1891a.
- ^ Minkowski 1891b.
- ^ Stickelberger 1897.
- ^ All facts in this paragraph can be found in Narkiewicz 2004, pp. 59, 81
- ^ a b Neukirch 1999, §III.2
- ^ Corollary III.2.10 of Neukirch 1999 or Proposition III.2.15 of Fröhlich & Taylor 1993
- ^ Voight 2008
- ^ Section 4.4 of Serre 1967
References
Primary sources
- Brill, Alexander von (1877), "Ueber die Discriminante", Mathematische Annalen 12 (1): 87–89, doi:10.1007/BF01442468, JFM 09.0059.02, MR1509928, http://gdz.sub.uni-goettingen.de/en/dms/load/toc/?PPN=PPN235181684_0012&DMDID=dmdlog8, retrieved 2009-08-22
- Dedekind, Richard (1871), Vorlesungen über Zahlentheorie von P.G. Lejeune Dirichlet (2 ed.), Vieweg, http://gdz.sub.uni-goettingen.de/en/dms/load/toc/?PPN=PPN30976923X&DMDID=dmdlog1, retrieved 2009-08-05
- Dedekind, Richard (1878), "Über den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Congruenzen", Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 23 (1), http://gdz.sub.uni-goettingen.de/en/dms/load/toc/?PPN=PPN250442582_0023&DMDID=dmdlog10, retrieved 2009-08-20
- Hermite, Charles (1857), "Extrait d'une lettre de M. C. Hermite à M. Borchardt sur le nombre limité d'irrationalités auxquelles se réduisent les racines des équations à coefficients entiers complexes d'un degré et d'un discriminant donnés", Crelle's Journal 53: 182–192, http://gdz.sub.uni-goettingen.de/dms/load/toc/?PPN=PPN243919689_0053&DMDID=dmdlog14, retrieved 2009-08-20
- Kronecker, Leopold (1882), "Grundzüge einer arithmetischen Theorie der algebraischen Grössen", Crelle's journal 92: 1–122, JFM 14.0038.02, http://gdz.sub.uni-goettingen.de/dms/load/toc/?PPN=PPN243919689_0092&DMDID=dmdlog4, retrieved 2009-08-20
- Minkowski, Hermann (1891a), "Ueber die positiven quadratischen Formen und über kettenbruchähnliche Algorithmen", Crelle's journal 107: 278–297, JFM 23.0212.01, http://gdz.sub.uni-goettingen.de/dms/load/toc/?PPN=PPN243919689_0107&DMDID=dmdlog25, retrieved 2009-08-20
- Minkowski, Hermann (1891b), "Théorèmes d'arithmétiques", Comptes rendus de l'Académie des sciences 112: 209–212, JFM 23.0214.01
- Stickelberger, Ludwig (1897), "Über eine neue Eigenschaft der Diskriminanten algebraischer Zahlkörper", Proceedings of the First International Congress of Mathematicians, Zürich, pp. 182–193, JFM 29.0172.03
Secondary sources
- Bourbaki, Nicolas (1994), Elements of the history of mathematics, Berlin: Springer-Verlag, ISBN 978-3-540-64767-6, MR1290116. Translated from the original French by John Meldrum
- Cohen, Henri (1993), A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138, Berlin, New York: Springer-Verlag, ISBN 978-3-540-55640-4, MR1228206
- Cohen, Henri; Diaz y Diaz, Francisco; Olivier, Michel (2002), "A Survey of Discriminant Counting", in Fieker, Claus; Kohel, David R., Algorithmic Number Theory, Proceedings, 5th International Syposium, ANTS-V, University of Sydney, July 2002, Lecture Notes in Computer Science, 2369, Berlin: Springer-Verlag, pp. 80–94, doi:10.1007/3-540-45455-1_7, ISBN 978-3-540-43863-2, ISSN 0302-9743, MR2041075, http://www.springerlink.com/content/2bl9qep1qb4k32vy/, retrieved 2009-08-19
- Fröhlich, Albrecht; Taylor, Martin (1993), Algebraic number theory, Cambridge Studies in Advanced Mathematics, 27, Cambridge University Press, ISBN 978-0-521-43834-6, MR1215934
- Narkiewicz, Władysław (2004), Elementary and analytic theory of algebraic numbers, Springer Monographs in Mathematics (3 ed.), Berlin: Springer-Verlag, ISBN 978-3-540-21902-6, MR2078267
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR1697859
- Serre, Jean-Pierre (1967), "Local class field theory", in Cassels, J. W. S.; Fröhlich, Albrecht, Algebraic Number Theory, Proceedings of an instructional conference at the University of Sussex, Brighton, 1965, London: Academic Press, ISBN 0-121-63251-2, MR0220701
- Voight, John (2008), "Enumeration of totally real number fields of bounded root discriminant", in van der Poorten, Alfred J.; Stein, Andreas, Algorithmic number theory. Proceedings, 8th International Symposium, ANTS-VIII, Banff, Canada, May 2008, Lecture Notes in Computer Science, 5011, Berlin: Springer-Verlag, pp. 268–281, arXiv:0802.0194, doi:10.1007/978-3-540-79456-1_18, ISBN 978-3-540-79455-4, MR2467853
- Washington, Lawrence (1997), Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, 83 (2 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94762-4, MR1421575
Further reading
- Milne, James S. (1998), Algebraic Number Theory, http://www.jmilne.org/math/CourseNotes/ant.html, retrieved 2008-08-20
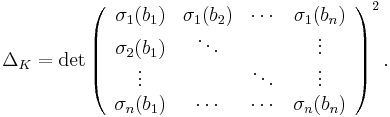
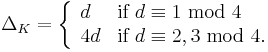
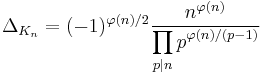
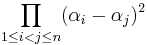
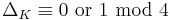
![\Delta_{K/F} = \mathcal{N}_{L/F}\left({\Delta_{K/L}}\right) \Delta_{L/F}^{[K:L]}](/2012-wikipedia_en_all_nopic_01_2012/I/fd217485cb125eb74ecac6ac77472718.png)